Embarking on the Basics: Exploring Units and Dimensions
In the realm of science and mathematics, World of Dimensional Formula Class11 helps us understand the fundamentals of units and dimensions. It serves as the cornerstone for all further exploration. Whether delving into physics, engineering, or any scientific discipline.
In the realm of physics and other scientific disciplines, quantities are categorized into two main types: fundamental and derived quantities.
Fundamental Quantities: World of Dimensional Formula Class11
- Cannot be expressed in terms of other physical quantities.
- Serve as the basis for measurement in a system.
- Defined by standard units.
- Examples include length, mass, time, electric current, temperature, amount of substance, and luminous intensity.
Derived Quantities: World of Dimensional Formula Class11
- Derived from fundamental quantities through mathematical operations or combinations.
- Express relationships between two or more fundamental quantities.
- Examples include speed (derived from distance and time), density (derived from mass and volume), and acceleration (derived from velocity and time).
- Crucial for formulating laws, equations, and theories in science.
Fundamental and supplementary physical quantities in the SI system
Fundamental Physical Quantities in the SI System: World of Dimensional Formula Class11
-
- Defined by the International System of Units (SI).
- Include seven fundamental quantities: length, mass, time, electric current, temperature, amount of substance, and luminous intensity.
- Serve as the foundation for measuring other physical quantities.
- Expressed in terms of standard SI units such as meters, kilograms, seconds, amperes, kelvin, moles, and candelas.
Supplementary Physical Quantities in the SI System: World of Dimensional Formula Class11
-
- Additional quantities derived from fundamental ones to enhance measurement precision or describe complex phenomena.
- Examples include plane angle (radian), solid angle (steradian), and frequency (hertz).
- Plane angle and solid angle supplement length and provide a means to measure rotation and spatial extent in three dimensions.
- Frequency complements time, indicating the number of cycles or occurrences per unit time.
- While not fundamental, these supplementary quantities play vital roles in various scientific and engineering applications within the SI framework
Supplementary Quantities: World of Dimensional Formula Class11
-
- Augment the fundamental quantities in the International System of Units (SI) to provide a more comprehensive framework for measurement.
- Include plane angle, solid angle, and frequency.
- Plane angle, measured in radians, supplements length by quantifying rotation or angular displacement.
- Solid angle, measured in steradians, complements length by quantifying spatial extent in three dimensions, crucial in fields like optics and astronomy.
- Frequency, measured in hertz (Hz), supplements time by indicating the number of cycles or occurrences per unit time interval, pivotal in fields such as telecommunications, physics, and engineering.
- While not considered fundamental, supplementary quantities play essential roles in various scientific and engineering disciplines, enriching the SI system and enabling precise measurements and analyses of physical phenomena.
What Are Dimensions? World of Dimensional Formula Class11
Dimensions represent the fundamental attributes or characteristics that define the nature of a physical quantity. In simpler terms, dimensions answer the question “what kind of quantity are we measuring?” For example, when measuring length, we’re concerned with one-dimensional aspects, while measuring an object’s volume introduces three dimensions—length, width, and height.
These dimensions provide a framework for quantifying and understanding the world around us, allowing scientists and researchers to categorize and analyze various phenomena.
In this way, dimensions serve as a foundational concept in physics and mathematics, enabling us to explore and comprehend the intricacies of the universe.
Dimensional Formula: World of Dimensional Formula Class11
The term “Dimensional Formula” refers to a method used in physics to express physical quantities in terms of their fundamental dimensions. It’s a way of representing a physical quantity in terms of the fundamental dimensions of mass, length, and time, denoted as [M], [L], and [T], respectively.
For example, the dimensional formula for velocity is [LT^-1], indicating that it has dimensions of length per unit time.
By understanding the dimensional formula of a quantity, scientists can gain deeper insights into its underlying properties and relationships with other physical quantities, facilitating further exploration and discovery in the field of physics.
Derivations of the dimensional formulae of all important physical quantities: World of Dimensional Formula Class11
In the study of chemistry at the 11th-grade level, understanding the dimensional formulae of important physical quantities is crucial for grasping the fundamental principles of the subject.
Here, we embark on a journey to derive the dimensional formulae for these key quantities, enabling a deeper comprehension of their significance and interrelationships.
Length (L): The dimensional formula for length is straightforward, denoted as [L], representing its fundamental dimension.
Mass (M): Similar to length, mass possesses its fundamental dimension, denoted as [M].
Time (T): Time also has its fundamental dimension, represented as [T].
Volume (V): Volume is derived from the fundamental dimensions of length cubed, denoted as [L^3].
Density (D): Density, being the mass per unit volume, is derived from the dimensions of mass divided by volume, represented as [M L^-3].
Velocity (v): Velocity is derived from the dimensions of length divided by time, denoted as [LT^-1].
Acceleration (a): Acceleration, representing the change in velocity over time, is derived from the dimensions of velocity divided by time, expressed as [LT^-2].
Force (F): Force, according to Newton’s second law (F = ma), is derived from the dimensions of mass multiplied by acceleration, represented as [MLT^-2].
Energy (E): Energy, being the capacity to do work, is derived from the dimensions of force multiplied by length, denoted as [ML^2T^-2].
Pressure (P): Pressure, defined as force per unit area, is derived from the dimensions of force divided by area, represented as [ML^-1T^-2].
Work (W): Work is the product of force and displacement, derived from the dimensions of force multiplied by length, denoted as [ML^2T^-2].
Power (P): Power, representing the rate at which work is done, is derived from the dimensions of work divided by time, expressed as [ML^2T^-3].
Electric Charge (Q): Electric charge, a fundamental property of matter, is derived from the dimensions of current multiplied by time, denoted as [IT].
Electric Potential (V): Electric potential, representing electric potential energy per unit charge, is derived from the dimensions of energy divided by electric charge, represented as [ML^2T^-2I^-1].
Electric Current (I): Electric current, the flow of electric charge, is derived from the dimensions of charge divided by time, expressed as [QT^-1].
Resistance (R): Resistance, hindering the flow of electric current, is derived from the dimensions of electric potential divided by current, denoted as [ML^2T^-3I^-2].
Capacitance (C): Capacitance, representing the ability to store electric charge, is derived from the dimensions of charge divided by electric potential, expressed as [IT^2M^-1L^-2].
Temperature (T): Temperature, a measure of the average kinetic energy of particles in a substance, is a fundamental physical quantity with its own dimension, denoted as [Θ].
Amount of Substance (n): The amount of substance, representing the number of particles in a sample, is another fundamental quantity with its own dimension, denoted as [N].
Molar Mass (M): Molar mass, the mass of one mole of a substance, is derived from the dimensions of mass divided by amount of substance, expressed as [M N^-1].
Molar Volume (V_m): Molar volume, representing the volume occupied by one mole of a substance, is derived from the dimensions of volume divided by amount of substance, denoted as [L^3 N^-1].
Heat Capacity (C): Heat capacity, representing the amount of heat required to raise the temperature of a substance by one degree Celsius, is derived from the dimensions of energy divided by temperature, denoted as [ML^2T^-2Θ^-1].
Specific Heat Capacity (c): Specific heat capacity, representing the amount of heat required to raise the temperature of one unit mass of a substance by one degree Celsius, is derived from the dimensions of energy divided by temperature and mass, expressed as [L^2T^-2Θ^-1M^-1].
Surface Tension (γ): Surface tension, representing the force per unit length required to stretch a liquid surface, is derived from the dimensions of force divided by length, denoted as [MT^-2].
Viscosity (η): Viscosity, representing a fluid’s resistance to flow, is derived from the dimensions of force multiplied by time divided by area, expressed as [ML^-1T^-1].
Wave Number (k): Wave number, representing the number of waves per unit length in a medium, is derived from the dimensions of angle divided by length, expressed as [L^-1].
Modulus of Elasticity (E): Modulus of elasticity, representing a material’s ability to deform under stress, is derived from the dimensions of force divided by area, denoted as [ML^-1T^-2].
Coefficient of Friction (μ): Coefficient of friction, representing the ratio of the force of friction between two surfaces to the force pressing them together, is derived from the dimensions of force divided by force, expressed as [ML^-1T^-2].
Atomic Mass Unit (u): Atomic mass unit, representing the mass of an individual atom, is derived from the dimensions of mass divided by amount of substance, represented as [M N^-1].
Half-Life (t_1/2): Half-life, representing the time required for half of a radioactive substance to decay, is derived from the dimensions of time, denoted as [T].
Activity (A): Activity, representing the rate of decay of a radioactive substance, is derived from the dimensions of radioactive decay per unit time, expressed as [T^-1].
Cross Section (σ): Cross section, representing the measure of the probability of a certain interaction between particles, is derived from the dimensions of area, denoted as [L^2].
Stress (σ): Stress, representing the force applied per unit area, is derived from the dimensions of force divided by area, expressed as [ML^-1T^-2].
Strain (ε): Strain, representing the change in length per unit length of an object when subjected to stress, is dimensionless.
Magnetic Field Strength (H): Magnetic field strength, a measure of the intensity of a magnetic field, is derived from the dimensions of force per unit current, represented as [MT^-2I^-1].
Magnetic Flux (Φ): Magnetic flux, the quantity of magnetic field passing through a surface, is derived from the dimensions of magnetic field strength multiplied by area, denoted as [ML^2T^-2I^-1].
Inductance (L): Inductance, the ability of a circuit to generate electromotive force, is derived from the dimensions of magnetic flux divided by current, expressed as [ML^2T^-2I^-2].
Entropy (S): Entropy, a measure of the disorder or randomness in a system, is derived from the dimensions of energy divided by temperature, represented as [ML^2T^-2Θ^-1].
Enthalpy (H): Enthalpy, representing the heat content of a system, is derived from the dimensions of energy, denoted as [ML^2T^-2].
Gibbs Free Energy (G): Gibbs free energy, a measure of the maximum reversible work that can be performed by a system at constant temperature and pressure, is derived from the dimensions of energy, expressed as [ML^2T^-2].
Heat Transfer Coefficient (k): Heat transfer coefficient, representing the rate of heat transfer through a material, is derived from the dimensions of energy divided by temperature, length, and time, represented as [MLT^-3Θ^-1].
Heat Transfer Coefficient (k): Heat transfer coefficient, representing the rate of heat transfer through a material, is derived from the dimensions of energy divided by temperature, length, and time, represented as [MLT^-3Θ^-1].
Conductivity (σ): Conductivity, representing the ability of a material to conduct electricity, is derived from the dimensions of current divided by electric potential multiplied by length, denoted as [M^-1L^3T^3I^-2].
Dielectric Constant (κ): Dielectric constant, a measure of a material’s ability to store electrical energy in an electric field, is derived from the dimensions of capacitance multiplied by length, represented as [M^-1L^-1T^2I^2].
Magnetic Susceptibility (χ): Magnetic susceptibility, representing the extent to which a material becomes magnetized when exposed to a magnetic field, is derived from the dimensions of magnetic field strength divided by magnetic field strength, denoted as [L^3M^-1].
Electric Field Strength (E): Electric field strength, representing the force experienced by a unit charge placed in an electric field, is derived from the dimensions of force divided by electric charge, denoted as [MLT^-3I^-1].
Magnetic Field (B): Magnetic field, representing the force experienced by a moving charge in a magnetic field, is derived from the dimensions of force divided by electric charge multiplied by velocity, expressed as [MT^-2I^-1].
Molar Conductivity (Λ_m): Molar conductivity, representing the conductivity of a solution containing one mole of solute, is derived from the dimensions of conductivity multiplied by volume and amount of substance, expressed as [ML^2T^-3I^-1N^-1].
Ionization Energy (E_i): Ionization energy, representing the energy required to remove an electron from an atom or molecule, is derived from the dimensions of energy, denoted as [ML^2T^-2].
By comprehensively understanding the dimensional formulae of these additional physical quantities relevant to chemistry and other scientific fields, students can enhance their problem-solving skills and deepen their understanding of various phenomena and processes.
What Are Dimensional Constants? World of Dimensional Formula Class11
Dimensional constants are fundamental physical quantities that possess fixed numerical values and are independent of any system of units used for measurement.
Unlike dimensional variables, which can vary depending on the units employed, dimensional constants remain constant regardless of the chosen unit system.
These constants are often associated with physical laws and relationships and play a crucial role in theoretical physics, engineering, and other scientific disciplines.
Examples of dimensional constants include
the speed of light in a vacuum (c), Planck’s constant (h), the gravitational constant (G), the elementary charge (e) etc.
Watch this Video-
Derivations of the dimensions of important constants: World of Dimensional Formula Class11
- Speed of Light (c):
- The dimensional formula of speed is [LT^-1], representing length per unit time. The speed of light, being a velocity, has the same dimensional formula as speed.
- Therefore, the dimensions of the speed of light, denoted as [c], are [LT^-1].
- Planck’s Constant (h):
- Planck’s constant relates energy to frequency in quantum mechanics, as given by the equation 𝐸=ℎ𝑓, where E is energy, h is Planck’s constant, and f is frequency.
- Rearranging the equation to solve for h, we have ℎ=𝐸𝑓.
- Energy has the dimensional formula [ML^2T^-2], and frequency has the dimensional formula [T^-1].
- Substituting the dimensional formulae into the equation, we find that the dimensions of Planck’s constant, denoted as [h], are [ML^2T^-1].
- Gravitational Constant (G):
- The gravitational constant relates the force of gravity to the masses of objects and the distance between them, as described by Newton’s law of universal gravitation.
- Using Newton’s law, 𝐹=𝐺⋅𝑚1⋅𝑚2𝑟2, where F is force, G is the gravitational constant, 𝑚1 and 𝑚2 are masses, and r is the distance between the centers of masses.
- Rearranging the equation to solve for G, we have 𝐺=𝐹⋅𝑟2𝑚1⋅𝑚2.
- Force has the dimensional formula [MLT^-2], and distance has the dimensional formula [L].
- Substituting the dimensional formulae into the equation, we find that the dimensions of the gravitational constant, denoted as [G], are [L^3M^-1T^-2].
- Boltzmann Constant (𝑘𝐵):
- The Boltzmann constant relates the average kinetic energy of particles in a gas to the temperature of the gas, as given by the equation 𝐸=𝑘𝐵⋅𝑇, where 𝐸 is energy, 𝑘𝐵 is the Boltzmann constant, and 𝑇 is temperature.
- Rearranging the equation to solve for 𝑘𝐵, we have 𝑘𝐵=𝐸𝑇.
- Energy has the dimensional formula [ML^2T^-2], and temperature has the dimensional formula [Θ].
- Substituting the dimensional formulae into the equation, we find that the dimensions of the Boltzmann constant, denoted as 𝑘𝐵, are [ML^2Θ^-1].
- Avogadro’s Number (𝑁𝐴):
- Avogadro’s number represents the number of atoms, molecules, or particles in one mole of a substance.
- Since Avogadro’s number is a count of particles, it is dimensionless.
- Faraday Constant (𝐹):
- The Faraday constant represents the amount of electric charge carried by one mole of electrons, and it is used in electrochemistry.
- Charge has the dimensional formula [IT].
- Since the Faraday constant is a count of charge per mole, its dimensions are [IT N^-1].
- Rydberg Constant (𝑅):
- The Rydberg constant is used in atomic physics to describe the wavelengths of spectral lines of hydrogen.
- It is derived from the fundamental constants of nature and has dimensions of [T^-1], representing frequency.
- Gas Constant (𝑅):
- The gas constant relates the energy of a gas to its temperature and pressure, as given by the ideal gas law equation 𝑃𝑉=𝑛𝑅𝑇, where 𝑃 is pressure, 𝑉 is volume, 𝑛 is the number of moles, 𝑇 is temperature, and 𝑅 is the gas constant.
- Rearranging the equation to solve for 𝑅, we have 𝑅=𝑃𝑉𝑛𝑇.
- Pressure has the dimensional formula [ML^-1T^-2], volume has the dimensional formula [L^3], amount of substance has the dimensional formula [N], and temperature has the dimensional formula [Θ].
- Substituting the dimensional formulae into the equation, we find that the dimensions of the gas constant, denoted as 𝑅, are [ML^2T^-2Θ^-1N^-1].
- Stefan-Boltzmann Constant (𝜎):
- The Stefan-Boltzmann constant relates the total power radiated by a black body to its temperature, as described by Stefan-Boltzmann law equation 𝑃=𝜎𝐴𝜀𝑇4, where 𝑃 is power, 𝐴 is the surface area, 𝜀 is the emissivity, 𝑇 is temperature, and 𝜎 is the Stefan-Boltzmann constant.
- Rearranging the equation to solve for 𝜎, we have 𝜎=𝑃𝐴𝜀𝑇4.
- Power has the dimensional formula [ML^2T^-3], surface area has the dimensional formula [L^2], emissivity is dimensionless, and temperature has the dimensional formula [Θ].
- Substituting the dimensional formulae into the equation, we find that the dimensions of the Stefan-Boltzmann constant, denoted as 𝜎, are [ML^2T^-3Θ^-4].
- Molar Gas Constant (𝑅):
- The molar gas constant, also known as the universal gas constant, is defined as the product of the Boltzmann constant and Avogadro’s number, and it is used in thermodynamics.
- Since the Boltzmann constant has dimensions [ML^2Θ^-1] and Avogadro’s number is dimensionless, the dimensions of the molar gas constant, denoted as 𝑅, are [ML^2Θ^-1N^-1].
- Permittivity of Free Space ():
- The permittivity of free space, also known as vacuum permittivity, is a fundamental constant in electromagnetism. It represents the ability of a vacuum to permit the transmission of electric fields.
- Permittivity has the dimensions of [M^-1L^-3T^4I^2], representing electric charge squared divided by force multiplied by length squared.
- Therefore, the dimensions of the permittivity of free space, denoted as 𝜀0, are [M^-1L^-3T^4I^2].
- Permeability of Free Space ():
- The permeability of free space, also known as vacuum permeability, is a fundamental constant in electromagnetism. It represents the ability of a vacuum to permit the transmission of magnetic fields.
- Permeability has the dimensions of [MLT^-2I^-2], representing force per unit current squared.
- Therefore, the dimensions of the permeability of free space, denoted as 𝜇0, are [MLT^-2I^-2].
- Electric Conductivity (𝜎):
- Electric conductivity represents the ability of a material to conduct electric current. It is the reciprocal of resistivity.
- Conductivity has the dimensions of [ML^-3T^3I^2], representing current per unit electric field multiplied by length.
- Therefore, the dimensions of electric conductivity, denoted as 𝜎, are [ML^-3T^3I^2].
- Magnetic Permeability (𝜇):
- Magnetic permeability represents the ability of a material to respond to an applied magnetic field.
It is the reciprocal of magnetic susceptibility.
- Permeability has the dimensions of [MLT^-2I^-2], representing force per unit current squared.
- Therefore, the dimensions of magnetic permeability, denoted as 𝜇, are [MLT^-2I^-2].
Watch this Video-
Some Examples of Dimensionless Quantities: World of Dimensional Formula Class11
Here are some examples of dimensionless quantities:
- Reynolds Number: Used in fluid mechanics, it represents the ratio of inertial forces to viscous forces in a fluid flow, determining whether the flow is laminar or turbulent.
- Mach Number: In aerodynamics, it denotes the ratio of the speed of an object to the speed of sound in the surrounding medium, indicating whether the object is traveling at subsonic, transonic, supersonic, or hypersonic speeds.
- Euler’s Number (e): In mathematics, it is a fundamental constant representing the base of the natural logarithm. It arises in various mathematical contexts, such as compound interest calculations and exponential growth.
- Aspect Ratio: In geometry, it refers to the ratio of the length of the longer side of a shape to the length of its shorter side. It characterizes the shape’s elongation or compactness and is widely used in engineering, architecture, and design.
- Refractive Index: In optics, it signifies the ratio of the speed of light in a vacuum to the speed of light in a given medium. It determines how much light is bent or refracted as it passes from one medium to another, such as air to glass.
- Prandtl Number: Another dimensionless quantity in fluid mechanics, it represents the ratio of momentum diffusivity to thermal diffusivity in a fluid flow. It describes the relative importance of momentum and heat transfer in a fluid.
- Coefficient of Friction: In mechanics, it denotes the ratio of the force of friction between two surfaces to the force pressing them together. It quantifies the resistance to motion between the surfaces and is crucial in designing mechanical systems.
Law of Homogeneity of Dimensions: World of Dimensional Formula Class11
The Law of Homogeneity of Dimensions is a fundamental principle in physics and mathematics that states that the dimensions of all terms in a mathematical equation must be consistent and compatible.
In simpler terms, it means that when performing mathematical operations or manipulations involving physical quantities, the dimensions on both sides of the equation must match.
One example of the Law of Homogeneity of Dimensions is demonstrated in the equation for velocity, 𝑣=𝑑/𝑡, where 𝑣 represents velocity, 𝑑 represents distance, and 𝑡 represents time.
According to the Law of Homogeneity of Dimensions, the dimensions of each term on both sides of the equation must be the same.
- The dimension of distance 𝑑 is represented by [L] (length), as it measures a linear displacement.
- The dimension of time 𝑡is represented by [T] (time), as it measures the duration of the motion.
- The dimension of velocity 𝑣 is represented by [LT^-1] (length divided by time), as it measures the rate of change of distance with respect to time.
When we substitute the dimensions into the equation, we have:
Dimension of L.H.S = [𝐿𝑇−1]
Dimension of R.H.S =[𝐿]/[𝑇]=
So, this equation satisfies the Law of Homogeneity of Dimensions.
It ensures that the equation is mathematically valid and physically meaningful, allowing for accurate interpretations and predictions in scientific analysis and experimentation.
Applications of Dimensional Analysis: World of Dimensional Formula Class11
Checking the Dimensional Consistency
Checking the Dimensional Consistency involves verifying whether the dimensions of all terms in an equation or expression are compatible with each other. This process ensures that the equation is mathematically valid and physically meaningful.
For instance,
consider the equation for the period 𝑇 of a simple pendulum:
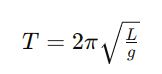
Where:
- 𝑇 is the period of the pendulum,
- 𝐿 is the length of the pendulum, and
- 𝑔 is the acceleration due to gravity.
To check the dimensional consistency of this equation, we assign dimensions to each term:
- The dimension of period 𝑇 is represented by [T] (time).
- The dimension of length 𝐿 is represented by [L] (length).
- The dimension of acceleration due to gravity 𝑔 is represented by [LT^-2] (length per time squared).
Substituting these dimensions into the equation:
Dimension of L.H.S = [
Dimension of R.H.S
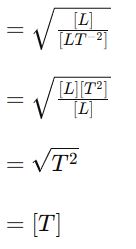
This confirms that the equation accurately represents the relationship between the period, length, and acceleration due to gravity of a simple pendulum.
Deducing the Relation among Physical Quantities using Dimensions: World of Dimensional Formula Class11
“Deducing the Relation among Physical Quantities using Dimensions” involves using the principle of dimensional analysis to derive relationships between different physical quantities based on their dimensions. This method is particularly useful when direct experimental measurements are unavailable or impractical.
Question:
FAQs: World of Dimensional Formula Class11
- Q: What is a dimensional formula?
- Answer: A dimensional formula represents the expression of a physical quantity in terms of its fundamental dimensions, such as length, mass, and time. It helps in understanding the nature of the physical quantity and its dependence on fundamental units.
- Q: How do you calculate dimensional formulae?
- Answer: To calculate the dimensional formula of a physical quantity, express it in terms of fundamental dimensions using its defining equation. Assign dimensions to each term in the equation and simplify to obtain the final dimensional formula.
- Q: Why are dimensional formulae important?
- Answer: Dimensional formulae play a crucial role in physics as they provide insights into the nature of physical quantities, help derive relationships among them, and facilitate dimensional analysis, which is essential for problem-solving and theoretical analysis.
- Q: Can dimensional analysis be used to check equations for correctness?
- Answer: Yes, dimensional analysis is a powerful tool for checking the correctness of equations. If the dimensions on both sides of an equation match, it indicates that the equation is dimensionally consistent and likely to be correct.
- Q: How are dimensional formulae applied in real-life scenarios?
- Answer: Dimensional formulae find applications in various fields such as engineering, chemistry, and physics. They are used to derive equations, predict physical behavior, design experiments, and analyze data, making them indispensable in scientific research and practical applications.
Also Read-
https://pcmconceptclear.com/best-book-for-science-class-11-cbse/
https://pcmconceptclear.com/best-science-book-for-class-11-isc/
https://pcmconceptclear.com/physics-class-11-units-and-measurement/
https://pcmconceptclear.com/some-basic-concepts-of-chemistry-cbse-11/
https://pcmconceptclear.com/mastering-mole-concepts-class-11/
9 thoughts on “World of Dimensional Formula Class11: Expert Tips(2025)”