Quantum Numbers and Electron Configuration: Chem11(2024)

What are Quantum Numbers?

In this blog post Quantum Numbers and Electron Configuration: Chem11(2024), We will study how Quantum numbers are the unique identifiers of electrons within an atom, much like addresses in a n, and spins of electrons in their atomic orbitals. These numbers are crucial in quantum  subatomic scale.

There are four types of quantum numbers:

1. Principal Quantum Number (n): Indicates the main energy level or shell of an electron.
2. Angular Momentum Quantum Number (l): Defines the shape of the orbital.
3. Magnetic Quantum Number (m_l): Specifies the orientation of the orbital in space.
4. Electron Spin Quantum Number (m_s): Denotes the spin direction of the electron.

Importance of Quantum Numbers and Electron Configuration in Quantum Mechanics

Quantum numbers are fundamental to understanding the complex world of quantum mechanics. They provide a detailed description of the position and energy of electrons in an atom, which is essential for Understanding Quantum Numbers and Electron Configuration.

Following are the main reasons- 

Predicting Electron Configuration:

Quantum numbers help determine how electrons are arranged in an atom, which is key to understanding the atom’s chemical properties and behavior.

Describing Atomic Orbitals:

Each set of quantum numbers corresponds to a specific atomic orbital, describing its size, shape, and orientation. This helps visualize where electrons are likely to be found.

Ensuring Unique Electron States:

According to the Pauli Exclusion Principle, no two electrons in an atom can have the same set of quantum numbers. This principle is crucial for maintaining the structure and stability of atoms.

Explaining Spectral Lines:

Quantum numbers explain the discrete energy levels of electrons and the transitions between these levels, which result in the emission or absorption of light at specific wavelengths. This phenomenon is observed in spectroscopy.

Understanding Chemical Bonding:

The arrangement and behavior of electrons, as described by quantum numbers, play a pivotal role in forming chemical bonds between atoms. This understanding is fundamental to chemistry and molecular physics.

In summary, quantum numbers are essential tools for scientists to unravel the mysteries of atomic structure and behavior. They provide a comprehensive framework for predicting and explaining a wide range of physical and chemical phenomena, making them indispensable in the field of quantum mechanics. This is equally important for understanding

Principal Quantum Number (n)

Definition

The principal quantum number, denoted by the letter ‘n,’ is a fundamental quantum number that specifies the main energy level or shell of an electron within an atom. It is always a positive integer (n = 1, 2, 3, …) and primarily determines the electron’s distance from the nucleus and its overall energy. The larger the value of ‘n,’ the higher the energy level and the further the electron is from the nucleus.

Significance in Atomic Structure & in Understanding Quantum Numbers and Electron Configuration

The principal quantum number is crucial for understanding the structure of an atom. It defines the major energy levels or shells in which electrons reside, effectively organizing electrons into layers around the nucleus. These energy levels are critical in several ways:

1. Energy Levels: The principal quantum number directly correlates with the energy level of an electron. Electrons in higher ‘n’ levels have more energy and are less tightly bound to the nucleus.
2. Electron Distribution: ‘n’ determines the number of electrons that can be accommodated within a particular shell. The maximum number of electrons in a shell is given by the formula 2n².
3. Chemical Properties: The energy levels indicated by ‘n’ influence an atom’s chemical behavior. Electrons in the outermost shell (highest ‘n’ value) are known as valence electrons, which play a key role in chemical reactions and bonding.

Examples and Calculation related with the Understanding of

Understanding the principal quantum number through examples and calculations can help clarify its role:

1. Hydrogen Atom: For a hydrogen atom, the principal quantum number ‘n’ can be 1, 2, 3, and so on. When n = 1, the electron is in the ground state, the closest and most stable energy level to the nucleus. If the electron absorbs energy and moves to n = 2, it transitions to a higher energy level, farther from the nucleus.
2. Electron Shells in Larger Atoms: In larger atoms, such as carbon, which has six electrons, the distribution among energy levels is as follows:
   • The first energy level (n = 1) can hold up to 2 electrons.
   • The second energy level (n = 2) can hold up to 8 electrons, but in the case of carbon, it holds the remaining 4 electrons.
3. Calculating Maximum Electrons:
   • For n = 1: Maximum electrons = 2(1)² = 2 electrons
   • For n = 2: Maximum electrons = 2(2)² = 8 electrons
   • For n = 3: Maximum electrons = 2(3)² = 18 electrons

These calculations show how the principal quantum number dictates the capacity of each energy level to accommodate electrons, thereby shaping the atom’s electron configuration and influencing its chemical properties.

In summary, the principal quantum number (n) is a key descriptor of the main energy levels in an atom, influencing electron energy, distribution, and the overall atomic structure. Understanding ‘n’ helps in grasping how electrons are organized within an atom and how this organization affects the atom’s chemical behavior and the understanding of Quantum Numbers and Electron Configuration.

Angular Momentum Quantum Number (l)

Definition

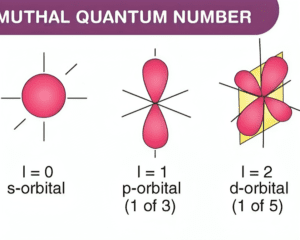
The angular momentum quantum number, symbolized by ‘l,’ is a quantum number that determines the shape of an electron’s orbital within an atom. It is also known as the azimuthal quantum number. The value of ‘l’ is an integer ranging from 0 to n-1, where ‘n’ is the principal quantum number. Each value of ‘l’ corresponds to a specific type of orbital, characterized by a distinct shape.

Role in Determining Orbital Shape

The angular momentum quantum number plays a crucial role in defining the geometry of an electron’s orbital. Here’s how different values of ‘l’ determine different orbital shapes:

1. s Orbital (l = 0): When ‘l’ is 0, the orbital is spherical in shape. Electrons in s orbitals are found in regions close to the nucleus and have no angular nodes.
2. p Orbital (l = 1): For ‘l’ equal to 1, the orbital is dumbbell-shaped. p orbitals have one angular node, a plane where the probability of finding an electron is zero. There are three p orbitals (px, py, pz) oriented along the x, y, and z axes.
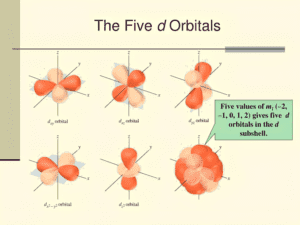
3. d Orbital (l = 2): When ‘l’ is 2, the orbitals take on more complex, cloverleaf shapes with two angular nodes. There are five d orbitals in each energy level from n=3 onwards.
4. f Orbital (l = 3): For ‘l’ equal to 3, the orbitals are even more complex in shape with three angular nodes. There are seven f orbitals in each energy level from n=4 onwards.

These shapes are crucial in determining the spatial distribution of electrons around the nucleus and influence the atom’s chemical bonding properties.

Relationship with Principal Quantum Number

The angular momentum quantum number ‘l’ is intrinsically linked to the principal quantum number ‘n’ in several ways:

1. Range of Values: For a given principal quantum number ‘n,’ the possible values of ‘l’ range from 0 to n-1. This means that if n = 3, ‘l’ can be 0, 1, or 2.
2. Subshells: Each value of ‘l’ within a particular energy level (n) defines a subshell. For instance, when n = 3:
   • l = 0 corresponds to the 3s subshell
   • l = 1 corresponds to the 3p subshell
   • l = 2 corresponds to the 3d subshell
3. Energy and Shape: The principal quantum number (n) determines the size and energy of the orbital, while the angular momentum quantum number (l) refines the shape of the orbital within that energy level. Higher values of ‘l’ within a given ‘n’ indicate more complex shapes and higher energy subshells.

In summary, the angular momentum quantum number (l) is essential for defining the shape of an electron’s orbital. It works in tandem with the principal quantum number (n) to detail the electron’s energy, shape, and orientation within an atom. Understanding ‘l’ helps elucidate the complex structures of electron orbitals and their impact on chemical bonding and molecular geometry. At the same time , it is crucial for understanding the concept of Quantum Numbers and Electron Configuration

Magnetic Quantum Number (m_l)

Definition

The magnetic quantum number, denoted as ‘m_l,’ is one of the four quantum numbers that describe the unique quantum state of an electron within an atom. The magnetic quantum number specifies the orientation of an electron’s orbital around the nucleus. Its values range from -l to +l, where ‘l’ is the angular momentum quantum number. Thus, for a given ‘l’, ‘m_l’ can take any integer value within this range, including zero.

Determining Orbital Orientation

The magnetic quantum number is crucial for determining the spatial orientation of an electron’s orbital. Each value of ‘m_l’ corresponds to a specific orientation of the orbital in three-dimensional space. Here’s how ‘m_l’ works for different types of orbitals:

1. s Orbital (l = 0): For ‘l’ = 0, the only possible value for ‘m_l’ is 0. This corresponds to the s orbital, which is spherically symmetric and does not have a specific orientation.
2. p Orbitals (l = 1): For ‘l’ = 1, ‘m_l’ can be -1, 0, or +1. These values correspond to the three p orbitals (px, py, pz), each oriented along a different axis (x, y, and z) in space.
3. d Orbitals (l = 2): For ‘l’ = 2, ‘m_l’ can be -2, -1, 0, +1, or +2. These five values correspond to the five d orbitals, each with a unique orientation and complex shape.
4. f Orbitals (l = 3): For ‘l’ = 3, ‘m_l’ ranges from -3 to +3, providing seven possible orientations for the seven f orbitals.

These orientations are essential for understanding how electrons occupy space around the nucleus and how they interact with external magnetic fields.

Examples and Calculation helpful to understand Quantum Numbers and Electron Configuration

To illustrate the role of the magnetic quantum number, let’s consider a few examples and calculations:

1. p Orbitals (l = 1):
   • For a p orbital, where ‘l’ = 1, ‘m_l’ can be -1, 0, or +1.
   • If ‘m_l’ = -1, the electron is in the px orbital.
   • If ‘m_l’ = 0, the electron is in the py orbital.
   • If ‘m_l’ = +1, the electron is in the pz orbital. Each of these orbitals is oriented along a different axis, demonstrating the different possible spatial orientations for electrons in p orbitals.
2. d Orbitals (l = 2):
   • For a d orbital, where ‘l’ = 2, ‘m_l’ can be -2, -1, 0, +1, or +2.
   • If ‘m_l’ = -2, the electron is in one of the five d orbitals, such as dxy.
   • If ‘m_l’ = -1, the electron might be in dxz.
   • If ‘m_l’ = 0, the electron could be in dzz.
   • If ‘m_l’ = +1, the electron might be in dyz.
   • If ‘m_l’ = +2, the electron could be in dx²-y². These values show how the five d orbitals each have unique orientations in three-dimensional space.
3. f Orbitals (l = 3):
   • For an f orbital, where ‘l’ = 3, ‘m_l’ ranges from -3 to +3.
   • This includes seven values: -3, -2, -1, 0, +1, +2, +3.
   • Each value corresponds to one of the seven uniquely shaped f orbitals.

In summary, the magnetic quantum number (m_l) is pivotal in determining the orientation of an electron’s orbital in space. By specifying the direction of orbitals, ‘m_l’ helps in understanding the spatial arrangement and behavior of electrons within atoms, influencing how atoms interact with each other and with external magnetic fields.

Electron Spin Quantum Number (m_s): So important for the concept of Quantum Numbers and Electron Configuration

Definition

The electron spin quantum number, symbolized as ‘m_s,’ is a quantum number that specifies the intrinsic angular momentum, or spin, of an electron within an atom. Unlike the other quantum numbers, which describe the electron’s position and energy, ‘m_s’ describes the direction of the electron’s spin. It can take one of two possible values: +1/2 or -1/2, often referred to as “spin-up” and “spin-down,” respectively.

Significance in Electron Configuration and in Understanding Quantum Numbers and Electron Configuration

The electron spin quantum number is crucial for understanding the detailed arrangement of electrons in atoms, known as electron configuration. Here’s why it is significant:

1. Pauli Exclusion Principle: This principle states that no two electrons in an atom can have the same set of four quantum numbers. Since each orbital can hold a maximum of two electrons, these electrons must have opposite spins (i.e., one with m_s = +1/2 and the other with m_s = -1/2). This ensures the uniqueness of each electron’s quantum state within an atom.
2. Magnetic Properties: The spin of electrons contributes to the magnetic properties of atoms and molecules. When electrons are paired (one spin-up and one spin-down), their magnetic effects cancel out. However, unpaired electrons (with the same spin) can create a net magnetic moment, influencing the atom’s overall magnetism.
3. Energy Levels: The electron spin quantum number affects the energy levels within an atom. In the presence of an external magnetic field, the spin states split into slightly different energy levels, a phenomenon known as spin splitting or Zeeman effect. This splitting is crucial in techniques like electron spin resonance (ESR) spectroscopy.

Spin States

The concept of spin states is integral to the understanding of electron behavior:

1. Spin-Up (m_s = +1/2): This state represents an electron spinning in one direction. It is often visualized as an arrow pointing upwards.
2. Spin-Down (m_s = -1/2): This state represents an electron spinning in the opposite direction to spin-up. It is visualized as an arrow pointing downwards.

When filling orbitals according to Hund’s rule, electrons first fill empty orbitals with the same spin (either all spin-up or all spin-down) before pairing up with electrons of the opposite spin. This minimizes electron-electron repulsion and leads to a more stable electron configuration.

For example, in a carbon atom with the electron configuration 1s² 2s² 2p²:

• The 1s and 2s orbitals each hold two electrons, with spins +1/2 and -1/2.
• The 2p orbital starts filling with two electrons, each in a separate p orbital with parallel spins (both either +1/2 or both -1/2), according to Hund’s rule.

In summary, the electron spin quantum number (m_s) is essential for defining the spin orientation of electrons, ensuring unique electron states within an atom, and influencing the atom’s magnetic properties and energy levels. Understanding ‘m_s’ is fundamental to grasping the complete picture of electron configuration and atomic behavior.

Relationship Between Quantum Numbers: A must know concept for Quantum Numbers and Electron Configuration

Interdependence of n, l, m_l, and m_s

Quantum numbers work together to provide a comprehensive description of an electron’s position and behavior within an atom. Here’s how these four quantum numbers—principal quantum number (n), angular momentum quantum number (l), magnetic quantum number (m_l), and electron spin quantum number (m_s)—are interrelated:

1. Principal Quantum Number (n): This number determines the electron’s primary energy level or shell. It is a positive integer (n = 1, 2, 3, …). The value of ‘n’ influences the possible values of the other quantum numbers.
2. Angular Momentum Quantum Number (l): For a given ‘n’, ‘l’ can take integer values ranging from 0 to n-1. This quantum number defines the shape of the orbital.
   • For n = 1, l = 0 (only one value, corresponding to an s orbital).
   • For n = 2, l = 0 or 1 (corresponding to s and p orbitals).
3. Magnetic Quantum Number (m_l): For a given ‘l’, ‘m_l’ can range from -l to +l, including zero. This quantum number specifies the orientation of the orbital in space.
   • For l = 1 (p orbitals), m_l can be -1, 0, or +1, corresponding to the three different orientations of p orbitals (px, py, pz).
4. Electron Spin Quantum Number (m_s): Independent of n, l, and m_l, ‘m_s’ can be either +1/2 or -1/2, indicating the two possible spin states of an electron (spin-up or spin-down).

Impact on Electron Positioning: Significant in the understanding of Quantum Numbers and Electron Configuration

The interdependence of these quantum numbers determines the unique position and behavior of each electron within an atom. Here’s how they collectively influence electron positioning:

1. Energy Levels and Sublevels:
   • The principal quantum number (n) sets the broad energy level.
   • Within each energy level, the angular momentum quantum number (l) defines sublevels (s, p, d, f).
   • For example, if n = 3, the possible sublevels are 3s (l = 0), 3p (l = 1), and 3d (l = 2).
2. Orbital Orientation:
   • The magnetic quantum number (m_l) specifies the orientation of these sublevels. In the 3d sublevel (l = 2), the orbitals can have five different orientations: m_l = -2, -1, 0, +1, +2.
3. Spin States:
   • Within each orbital, the electron spin quantum number (m_s) ensures that no two electrons have the same set of four quantum numbers. This is essential for maintaining the Pauli Exclusion Principle, which states that no two electrons can occupy the same quantum state simultaneously.
   • In a 3d orbital, each specific orientation (m_l value) can hold two electrons with opposite spins (one with m_s = +1/2 and one with m_s = -1/2).
4. Electron Configuration:
   • The combined effect of these quantum numbers determines the electron configuration of an atom. For instance, the electron configuration of carbon (1s² 2s² 2p²) shows how electrons fill available orbitals based on these quantum numbers.
   • Electrons first fill lower energy orbitals (defined by n and l) and then occupy available orientations (m_l) and spin states (m_s).

The relationship between these quantum numbers ensures a unique and specific arrangement of electrons within an atom, influencing the atom’s overall stability, chemical properties, and behavior in various physical contexts. Understanding how n, l, m_l, and m_s interact provides a deeper insight into the quantum mechanical model of the atom.

Quantum Numbers and Electron Configuration

Aufbau Principle

The electron configuration of an atom refers to the arrangement of electrons within its atomic orbitals. Quantum numbers play a crucial role in determining electron configuration, guided by three fundamental principles:

1. Aufbau Principle: This principle states that electrons fill atomic orbitals from lowest to highest energy levels. In other words, electrons occupy the lowest energy orbitals available before filling higher energy levels. This principle is based on the increasing order of principal quantum numbers (n), with lower ‘n’ values corresponding to lower energy levels.
2. Pauli Exclusion Principle: According to this principle, no two electrons in an atom can have the same set of four quantum numbers. This means that each electron within an atom must have a unique combination of quantum numbers, ensuring that no two electrons occupy the same quantum state simultaneously.
3. Hund’s Rule: Hund’s rule dictates that when filling orbitals of equal energy (degenerate orbitals), electrons occupy them singly with parallel spins before pairing up. This minimizes electron-electron repulsion and stabilizes the electron configuration. Hund’s rule is based on maximizing the number of unpaired electrons, which leads to greater stability.

Application in Electron Configuration

The application of these principles in electron configuration follows a systematic approach:

1. Aufbau Principle: Electrons are added to orbitals starting from the lowest energy level (n = 1) and progressing to higher energy levels. Within each energy level, orbitals are filled according to their increasing energy, which corresponds to increasing values of the principal quantum number (n).
   • For example, in the electron configuration of carbon (C), the 1s orbital is filled first, followed by the 2s orbital, and then the 2p orbitals.
2. Pauli Exclusion Principle: Each orbital can hold a maximum of two electrons, each with opposite spins. This principle ensures that electrons within the same orbital have different spin states (m_s values), preventing electron-electron repulsion.
   • For instance, in the carbon atom, the 2p orbital can accommodate a maximum of six electrons, with each of the three p orbitals containing two electrons, each with opposite spins.
3. Hund’s Rule: When filling degenerate orbitals (orbitals with the same energy), electrons enter singly with parallel spins before pairing up. This rule maximizes the number of unpaired electrons, which contributes to the stability of the atom.
   • In carbon’s 2p sublevel, each of the three p orbitals initially receives one electron with parallel spins (Hund’s rule) before any orbital receives a second electron with opposite spin.

Conclusion: Quantum Numbers and Electron Configuration

In summary, quantum numbers are fundamental in determining the electron configuration of atoms. The Aufbau principle guides the order in which orbitals are filled, the Pauli exclusion principle ensures that no two electrons in an atom have the same set of quantum numbers, and Hund’s rule governs the filling of degenerate orbitals. Understanding these principles is essential for predicting the arrangement of electrons within atoms and explaining the properties and behaviors of elements in the periodic table.

FAQs

1. What is the Principal Quantum Number?
   • The principal quantum number, denoted by ‘n,’ is a quantum number that describes the main energy level or shell of an electron within an atom. It determines the size and energy of an electron’s orbital, with higher values of ‘n’ corresponding to higher energy levels and orbitals farther from the nucleus.
2. How are Quantum Numbers Used in Chemistry?
   • Quantum numbers are extensively used in chemistry to describe the behavior and properties of atoms and molecules. They play a crucial role in determining electron configurations, predicting chemical reactivity, understanding molecular geometry, and interpreting spectroscopic data. Quantum numbers provide a framework for understanding the electronic structure of elements and their interactions in chemical reactions.
3. What is the Difference Between l and m_l?
   • The quantum number ‘l’ (angular momentum quantum number) defines the shape of an electron’s orbital, while ‘m_l’ (magnetic quantum number) specifies the orientation of the orbital in space. ‘l’ takes integer values ranging from 0 to n-1, where ‘n’ is the principal quantum number, while ‘m_l’ can range from -l to +l, including zero.
4. How Do Quantum Numbers Affect Electron Configuration?
   • Quantum numbers dictate the arrangement of electrons within an atom’s orbitals, known as electron configuration. The principal quantum number ‘n’ determines the energy level or shell of the orbital, while the angular momentum quantum number ‘l’ defines the shape of the orbital. The magnetic quantum number ‘m_l’ specifies the orientation of the orbital, and the electron spin quantum number ‘m_s’ determines the spin state of the electron. Together, these quantum numbers determine the unique positioning of electrons in an atom.
5. Can Quantum Numbers be the Same for Different Electrons?
   • No, according to the Pauli Exclusion Principle, no two electrons in an atom can have the same set of four quantum numbers. While some quantum numbers may be the same for different electrons within an atom (such as ‘n’ for electrons in the same energy level), each electron must have a unique combination of quantum numbers. This principle ensures the distinct identity and behavior of each electron within an atom.

Watch This Video-

Also Read-

https://pcmconceptclear.com/mystery-of-atomic-orbitals/

https://pcmconceptclear.com/bohrs-atomic-model/

https://pcmconceptclear.com/rutherfords-nuclear-model-of-atom/

https://pcmconceptclear.com/mole-concept-iit-jee-pyqs-with-solutions/

https://pcmconceptclear.com/mastering-mole-concepts-class-11/

https://pcmconceptclear.com/some-basic-concepts-of-chemistry-cbse-11/

https://pcmconceptclear.com/acids-bases-salts-most-imp-qa/

https://pcmconceptclear.com/chemical-reactions-and-equations-class-10-science/

https://pcmconceptclear.com/electricity-class-10-made-easy/

https://pcmconceptclear.com/world-of-dimensional-formula-class11/